Detailed Description

We have total n products available numbered from \(1\) to \(n\). Each product belongs to one of the \(k\) categories and one of the \(m\) brands. Each product also has a base earning power \(c\). All products in the same category can be of a different brand, and the same brand can have multiple products in various categories.

The solution arranges products on a stand. The stand represents a rectangle with \(h\) shelves (rows), each one containing \(w\) positions (columns). Any product can occupy any position on any shelf. Any product occupies a single position, and any position can hold only one product. It is allowed to leave some products unplaced, as well as leave some positions unoccupied.

The resulting arrangement must comply with the following requirements to satisfy the visual convenience. Consider category \(t\), where at least one product is already on the shelf. Then, all positions occupied by other products of the same category \(t\) should form a continuous rectangle. We can express it in a more formally. Let us number the shelves from top to bottom with numbers from \(1\) to \(h\), and positions on each shelf from left to right with numbers from \(1\) to \(w\). Let \(a_l\) and \(a_r\) be the smallest and the largest number of shelves that present at least one product of category \(t\). Let \(b_l\) and \(b_r\) be the smallest and the largest number of positions among presented products. Then for any shelf \( a \, (a_l \leq a \leq a_r) \) and any position \(b \, (b_l \leq b \leq b_r)\), position \(b\) on the shelf a should have a product in category \(t\).

Examples

Let \(h = w = 4\), and \(k = 3\). Consider the following arrangement (the numbers represent positions occupied by products from those categories; dots represent empty positions):

11.4
112.
..2.
..2.

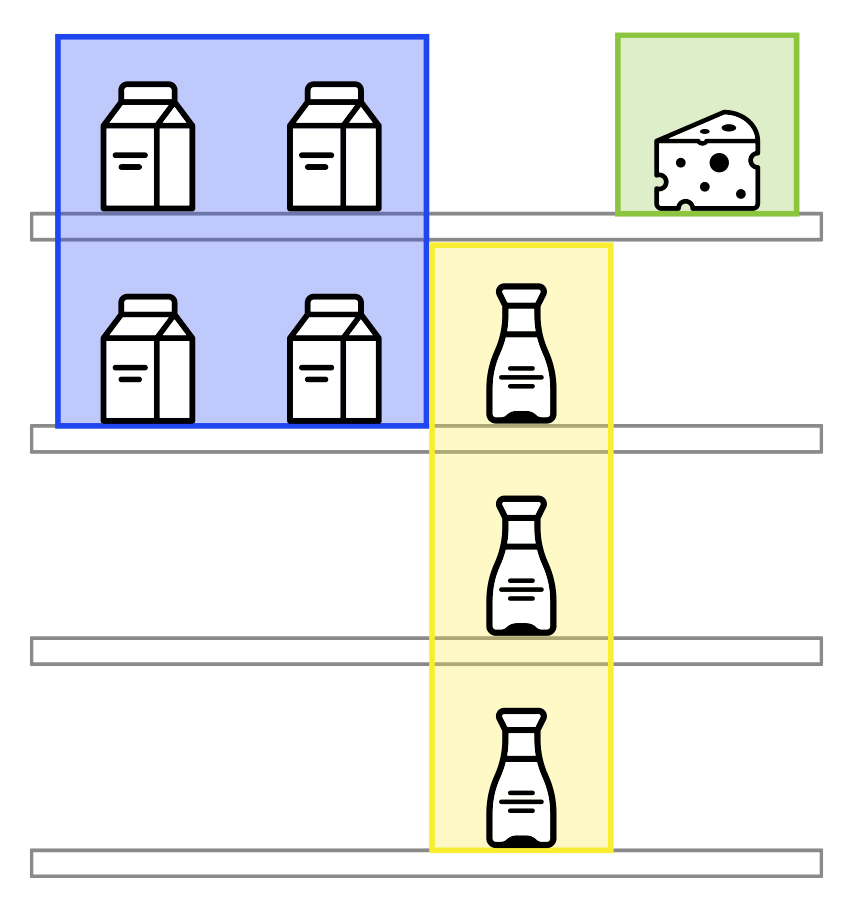
This arrangement is correct because positions of products in categories 1, 2, and 4 form a continuous rectangle and there are no products of category 3.

Here’s another example:

1111
1231
1241
1111

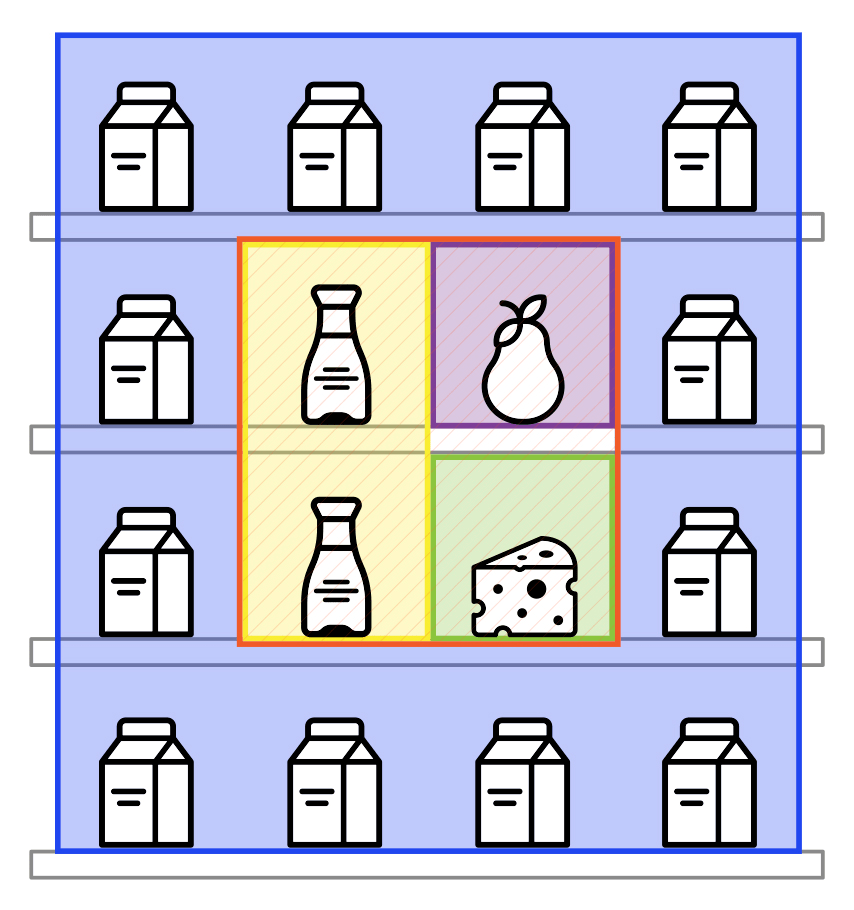
This arrangement is incorrect, due to the fact that the products of category 1 do not occupy a continuous rectangle.

Input Format

The first input line provides six integer numbers \(n, k, m, h, w, D_0\). The numbers have the following limitations:

• \(1 \leq n \leq 5000\);
• \(1 \leq k,m \leq 50\);
• \(1 \leq h \leq 10\);
• \(1 \leq w \leq 100\);
• \(1 \leq D_0 \leq 106).

The next \(n\) lines describe the product parameters. Each i-th line has three integer numbers \(t_i\), \(b_i\), and \( c_i \, (1 \leq t_i \leq k, 1 \leq b_i \leq m, 1 \leq ci \leq 1000) \) — correspondingly, category, brand, and the base earning power of the product.

Output Format

The solution must output \(h\) lines, each line containing \(w\) integer numbers separated by space. The number in position \(j\) on the line \(i\) should be equal to 0 if the position \(j\) on the shelf \(i\) is empty, otherwise, it should be equal to the product’s number in this position.

Tests Generation Algorithm

It is guaranteed that every test in the tests set is generated using the following algorithm.

The following parameters are picked manually:

• \(h,\, w,\, n,\, k,\, m,\, D_0\);
• frequency criterion pi and brand frequency criterion \( q_i \, (p_i + q_i = 1 \, \text{for all} \, i) \);
• base earning power for goods categories \(A_i\) and goods brands \(B_i\).

For each brand, the algorithm randomly selects up to 10 various categories for goods (the minimal possible amount of categories is 1). The number of products can be selected manually.

Then, \(n\) products are generated independently according to the following scheme:

1. The category \(t\) and brand \(b\) are picked randomly and independently according to distributions determined by \(p_i\) and \(q_i\) params;
2. If the brand \(b\) does not produce category \(t\), go back to step 1.
3. Assign base earning power for this product as \(c = \text{round}(\xi(A_t + B_b))\), where \(\xi\) — is a random value from the range [0.5, 1], and round is a math rounding function.

Quality Criteria

The program will be run for every test in the tests set. Overall score equals to the sum of scores for each test in the tests set.

Solution is scored for each test with the following formula:

$$C = D_0 \sum_{j=1}^k \sqrt{\frac{q_j}{h \times w}} + \sum_{i=1}^n I_i c_i (1 + \log_2 A_i)$$

If the program ran out of time or the result was incorrect then the score for that test is \(C = 0\).

In the formula above, the following notation is used:

• \(D_0\) — provided initial variety bonus coefficient;
• \(q_j\) — amount of arranged products in j category;
• \(I_i\) is 1 if the product \(i\) was arranged and 0 otherwise;
• \(c_i\) — provided base earning power of a product \(i\);
• \(A_i\) — the maximum number of positions in a continuous rectangle, filled with products of the same brand and including product \(i\).

Evaluation Example

Let \( h = w = 4, \, n = 9, \, k = m = 3, \, D_0 = 50 \). SKU parameters are defined with the following arrays:

• Categories \(t = [1,1,1,1,2,2,2,3,3]\);
• Brands \(b = [1,1,2,3,1,1,3,2,2]\);
• Base earning power \(c = [2, 3, 5, 10, 4, 3, 9, 6, 7]\).

Consider the following arrangement method:

.567
.12.
.438
...9

Categories, brands and \(A_i\) are distributed in the following fashion:

.222   .113   .441   
.11.   .11.   .44.   
.113   .322   .122   
...3   ...2   ...2

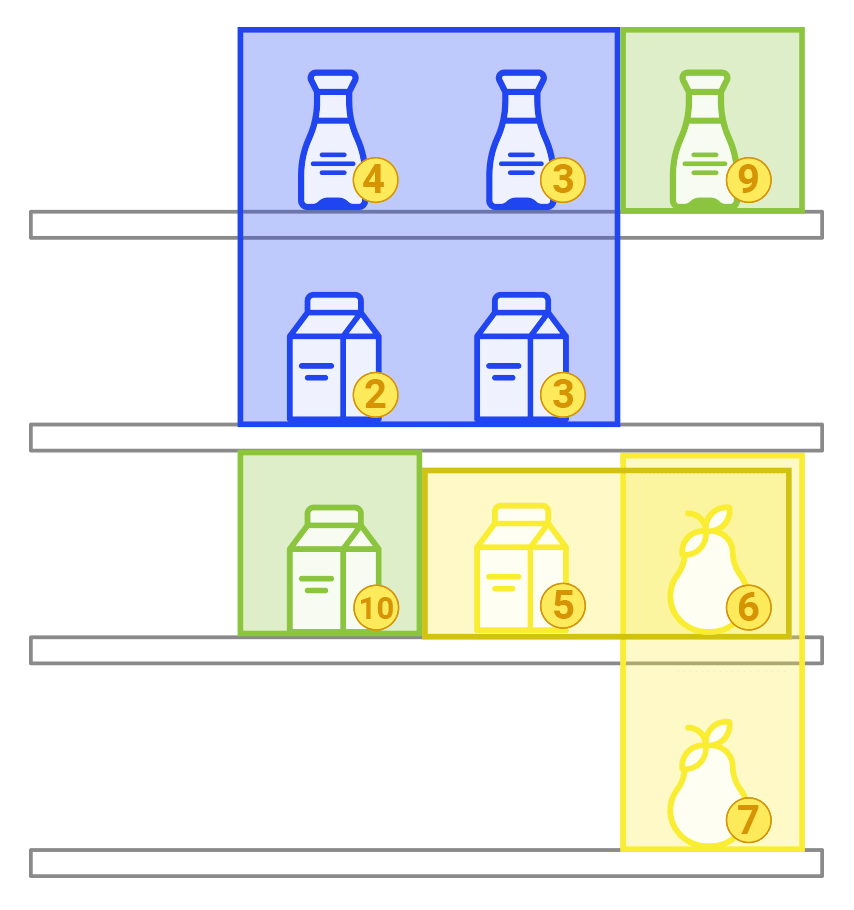
The values of \(q_j\) are equals to: \(q_1 = 4,\, q_2 = 3,\, q_3 = 2\). Variety bonus \(D \approx 64.328\). Effective profit \(E\) is equals to 91 and overall score is \(C = D + E \approx 155.328\).

Submission Format

Participants expected to send the submission’s code to the grading system. The file extension of submission determines the way the execution and the following evaluation will be performed.

There are two possible options:

1. Single-module solution

This is similar to ACM ICPC scheme. One can use Python3, Java, or C++. The module is compiled to a binary executable and then tests are carried out. Solution should have one of the following file extensions: .py, .java, or .cpp.

2. Submitting algorithm code as an archive

Submission is expected to be a ZIP archive with all files necessary to execute the solution. The root directory of the archive must contain a metadata.json file with the following content:

{"image": "datasouls/python","entry_point": "python solution.py"}

Where image is a field used to describe docker-image used as a base image to run your solution. The field entry_point contains a command to start a solution. The current during runtime is the root of the archive (the same directory where metadata.json is located).

Solutions are executed in an isolated docker environment with imposed limitations on both available resources and execution time during testing.

The archive can contain compiled binary files, but the source code and detailed build instructions should be also present. All potentially winning solutions will be checked manually for reproducibility.

Technical Limitations

Solutions are executed in an isolated docker environment under the following conditions:

• Each solution has access to 1 Gb RAM and 4 vCPUs;
• Solutions have no access to the Internet;
• Each test must finish in 15 seconds;
• Maximum submission size of solution’s archive is 256 Mb (both packed and unpacked)